Resumen
Cada año toca la difícil y subestimada tarea de revisión del desempeño de los trabajadores en la empresa. Cada empleado es evaluado por sus superiores y encasillado en un "slot" que, según los modelos clásicos, nos llevan a una distribución normal. Pero, ¿Sigue el desempeño de la plantilla una distribución normal?
----ooooOOOOoooo----
Actualmente existe la creencia en muchas empresas que el rendimiento de los trabajadores se puede ajustar a una distribución normal (curva de Gauss). Estudios recientes demuestran que este “dogma de fe” está seriamente comprometido y, que la distribución de Gauss no refleja la realidad de una empresa. Pese a ello, a día de hoy muchas empresas continúan haciendo "normal" el talento original de la individualidad del capital humano.
A continuación se expondrán dos puntos de vista de un mismo problema, la gestión del desempeño.
A continuación se expondrán dos puntos de vista de un mismo problema, la gestión del desempeño.
- Teoría clásica: Se asume como irrefutable la distribución normal y se ajusta el desempeño de los trabajadores para que quede bajo la curva.
- Nuevas tendencias: Se evalúa el desempeño real de los trabajadores y se realiza un contraste de hipótesis para ver qué distribución estadística es la más acertada al desempeño de la plantilla.
1. Teoría clásica para la gestión del desempeño (distribución normal)
Desde principios del siglo pasado, la estadística evolucionó de manera considerable y con ello la aplicación al mundo de la empresa. En estos inicios de la industria donde abundaba la mano de obra no cualificada, con el apoyo de la teoría de los grandes números y el teorema central del límite, se estableció que la gestión del desempeño de los trabajadores se ajustaba a una distribución normal y actualmente, este criterio continúa vigente en muchas empresas.
Siguiendo esta corriente, si durante el proceso de evaluación se observa que el desempeño de los trabajadores no se ajusta a una normal, RRHH atribuye el problema a una serie de factores subjetivos como una evaluación benevolente, severa o errores de halo. Ante esa situación, se modifican los resultados y, bajo ningún pretexto se cuestiona si realmente el desempeño se puede ajustar mejor a otro modelo estadístico. Estudios recientes demuestran que hoy en día, esta asunción es muy discutible aunque muchas empresas (y no precisamente pequeñas) aún la siguen siguen aplicando.
Siguiendo esta corriente, si durante el proceso de evaluación se observa que el desempeño de los trabajadores no se ajusta a una normal, RRHH atribuye el problema a una serie de factores subjetivos como una evaluación benevolente, severa o errores de halo. Ante esa situación, se modifican los resultados y, bajo ningún pretexto se cuestiona si realmente el desempeño se puede ajustar mejor a otro modelo estadístico. Estudios recientes demuestran que hoy en día, esta asunción es muy discutible aunque muchas empresas (y no precisamente pequeñas) aún la siguen siguen aplicando.
Acorde al modelo de la distribución normal, el desempeño de los trabajadores se puede ajustar en torno a la media de desempeño de toda la plantilla. Según éste modelo, la plantilla se distribuye según:
- Rango 1: Un 2.28 % tiene un rendimiento mediocre. Correspondiente al intervalo [-inf ,-2 sigma]
- Rango 2: Un 13.59 % tiene un rendimiento inferior a la media. Correspondiente al intervalo [-2 sigma , -1 sigma]
- Rango 3: Un 68.26 % tiene un rendimiento en la media. Correspondiente al intervalo [-1 sigma , 1 sigma]
- Rango 4: Un 13.59 % tiene un rendimiento superior a la media. Corresponde al rango [1 sigma , 2 sigma]
- Rango 5: Un 2.28 % tiene un rendimiento excelente. Correspondiente al intervalo [2 sigma , Inf]
 |
| Fig.1 - Distribución normal del desempeño |
Cabe destacar que a ambos lados de la media y en iguales proporciones, se encuentran los trabajadores con un rendimiento superior a la media (lado derecho) y los trabajadores con un rendimiento inferior a la media (lado izquierdo).
1.1- Ventajas
- No es necesario un análisis previo del desempeño de la plantilla. Se supone que el desempeño de esta sigue una distribución normal facilitando los cálculos estadísticos y haciendo la vida fácil al departamento de RRHH.
- Si el desempeño sigue una curva normal, entonces es bastante fácil prever las compensaciones basadas en el rendimiento ya que la distribución de los trabajadores está claramente predeterminada independientemente de la realidad. Es decir, se puede calcular la partida presupuestaria para incremento salarial independientemente de la evaluación real del talento.
1.2- Inconvenientes
- Acorde a la distribución normal, estamos recortando el número de empleados etiquetados con rendimiento excelente. Muchas empresas establecen criterios a la hora de evaluar. Si se usa una escala del 1 al 5, dicen... “no puede haber más del 3 % de la plantilla en el rango excelente (rango 5) y, forzosamente tiene que haber un 3 % de la misma con en el rango mediocre (rango 1)
- Se fuerza a que el 16 % de la plantilla esté en el rango inferior a la media, los perdedores del grupo. Pero… ¿Qué pasa si el equipo de trabajo es el mejor que podemos tener? Aun así, aunque tengamos a los mejores trabajadores que puede haber en el mercado con nosotros, estamos forzando a que un 16 % de ellos estén catalogados como “poco útiles” originando frustraciones, malestar y muy posiblemente fugas de conocimiento de la empresa ya que a esos empleados no se les retribuirá en consecuencia.
- La distribución normal debe incluir a una población completa, sin sesgar, lo que no ocurre en las empresas, ya que el departamento de RRHH se encarga de hacer la selección del personal en la contratación buscando a los mejores perfiles. Estos profesionales fuerzan el sesgo de la distribución promocionando el talento y desincentivando a su vez la mediocridad. Buscan la élite entre la multitud de candidatos y, por lo tanto, la población analizada no está distribuida de manera aleatoria tal y como Dios nos trajo al mundo, violando así la hipótesis de partida de la estadística.
- Distribución forzada: ¿y si el desempeño no sigue una distribución normal? ¿Estamos falseando la realidad? La respuesta es un rotundo SÍ. La distribución normal obliga a las empresas a hacer una distribución forzada de sus recursos para poder construir la curva. Los empleados son encasillados en “slots” y todos los "slots" deben estar rellenos con un número predefinido independientemente del desempeño de la plantilla. Se asume que el desempeño sigue una distribución normal como un acto de fe.
- Siempre hay perdedores: imaginemos ahora que a los trabajadores que están en el rango 1 (los perdedores) los despedimos y, no hay nuevas contrataciones en la empresa. Seis meses después, se procede a hacer una nueva evaluación acorde a la distribución normal (véase figura 2) Claramente, se ve que la media de la plantilla ha mejorado en rendimiento, pero de nuevo vuelve a haber “slots” para perdedores (que antes no lo eran) y el número de trabajadores en rango 5 (excelentes) desciende originando la frustración del personal que realmente aporta a la empresa. Sorprendente ejercicio ¿verdad?
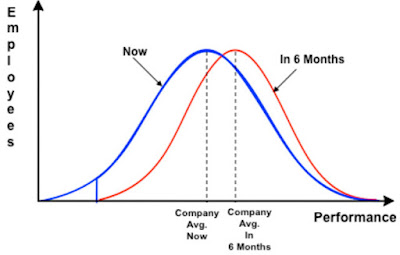 |
| Fig.2- Distribución normal del desempeño y los perdedores |
1.3 La distribución forzada y la frustración en la plantilla
Los empleados evaluados bajo una distribución forzada a la normal podrían estar afectados por los siguientes puntos:
- Búsqueda del protagonismo individual y disminución de la colaboración en el grupo. ¿Por qué colaborar cuando compito contra mi compañero?
- El personal en rango 4 (siendo 5 el máximo sobre 5), muchas veces son personal de alto potencial que se sienten frustrados porque, aun mereciéndolo, ese año no han podido (o no les ha correspondido) el 5 por temas de “cupo”.
- El personal en rango 3 muchas veces son personas que, sabiendo que no van a poder ser 4 o 5, no aspiran a ello y, simplemente se quedan en su zona de confort, no aspirando a mejora personal, ni por supuesto, a su mejor desempeño dentro de la empresa.
- En términos económicos, el grueso de la compensación generalmente se reparte entre ese 68 % de la media y, se limitan las posibilidades de dar mayores salarios a las personas que realmente contribuyen más a la empresa….¡¡ Cuidado….ser justos no significa ser iguales!!
- No fomenta la mejora continua, ya que el número 5 está muy limitado, con lo que en muchos casos ¿Para qué competir si ya sé a quién se lo van a dar?
Resumiendo y con todo lo expuesto, ¿es la distribución normal una herramienta justa de evaluación del talento? O por el contrario su uso genera frustraciones, desmotivación en personas de valía y, como consecuencia, posibles fugas de talento en la empresa.
2. Nuevos enfoques para la gestión del desempeño (Distribución de Pareto)
Tras lo expuesto en el punto anterior, ¿sigue el mundo real del desempeño una distribución normal? La respuesta es claramente NO.
Según un estudio realizado entre los años 2011 y 2012 por Ernest O’Boyle Jr. y Herman Aguinis (198 muestras repartidas en 633,263 investigadores, artistas, políticos y atletas profesionales), el desempeño sigue una distribución exponencial que se asemeja a la de Pareto. Basándose en las muestras del estudio, el 94 % de las ocasiones se encontró que el desempeño de los grupos analizados no seguía una distribución normal. En su lugar, la distribución se ajustaba a una de Pareto. Para el estudio, Ernest O’Boyle Jr. y Herman Aguinis utilizaron técnicas estadísticas de contraste de hipótesis para comparar la muestra de población con las distribuciones normal y de Pareto observando casi un perfecto ajuste a esta última y total disonancia con la "normal"
En la realidad de cualquier empresa suele haber:
- Un porcentaje mínimo que son extraordinarios y que realmente marcan la diferencia.
- Otro porcentaje muy cerca del anterior que son los que ayudan a marcar esa diferencia (entre ambos quizá suman el 20%)
- Resto de personas que con distinto rendimiento (nada de simetrías), se distribuye a lo largo de una curva “Long Tail”.
En esta situación, las evaluaciones se forzarían únicamente para homogeneizar los criterios de evaluación y no para buscar la simetría de una distribución. Lo que se buscaría con ella sería:
- Realmente identificar a ese porcentaje crítico que son los que con su trabajo y talento marcan la diferencia en la empresa.
- Poder hacer una distribución salarial más acorde a esa criticidad, de forma que la mayoría de la retribución no esté repartida en los “average” sino en los que realmente hacen que la empresa sea exitosa.
- Tener una distribución mucho más ajustada a lo que es la realidad de la empresa, y no a algo puramente estadístico e “igualitario”
- Reducir las frustraciones y los inconvenientes ocasionados que se producen al utilizar distribución normal.
3.- Conclusiones
- Cada empresa debería cuestionar la verdadera distribución estadística del desempeño de su plantilla. Para ello, en lugar de asumir a pie juntillas la validez de la distribución normal, se debería hacer un estudio estadístico del desempeño apoyado en un contraste de hipótesis contra una distribución de Pareto o similar.
- El salario de un trabajador no debe estar limitado por el tipo de trabajo que desarrolla sino por el valor que aporta a la empresa.
- Actualmente, los departamentos de RRHH de grandes compañías como Google o Microsoft se han dado cuenta que la verdadera distribución del desempeño de sus trabajadores no se podía forzar a una distribución normal sin cometer injusticias. Por ello, recientemente han adoptado distribuciones más ajustadas a la realidad como la de Pareto.
Como dijo el cabeza de Recursos Humanos de Google Laszlo Bock en su libro Work rules (2015):
“you should pay employees what they're worth, not for the job they do. It's hard work to have pay ranges where someone can make two or even 10 times more than someone else," he writes. "But it's much harder to watch your highest-potential and best people walk out the door. It makes you wonder which companies are really paying unfairly: the ones where the best people make far more than average, or the ones where everyone is paid the same."
"Se debería pagar a los empleados por lo que valen y no por el trabajo que hacen. Es un trabajo duro tener que pagar salarios donde alguien puede ganar dos o 10 veces más que otro" escribe. "Pero es mucho más duro ver como el alto potencial y la mejor gente se va por la puerta. Esto te hace pensar sobre qué empresas realmente están pagando injustamente: aquellas donde la mejor gente gana más que el promedio, o en las que todo el mundo gana lo mismo"
"Se debería pagar a los empleados por lo que valen y no por el trabajo que hacen. Es un trabajo duro tener que pagar salarios donde alguien puede ganar dos o 10 veces más que otro" escribe. "Pero es mucho más duro ver como el alto potencial y la mejor gente se va por la puerta. Esto te hace pensar sobre qué empresas realmente están pagando injustamente: aquellas donde la mejor gente gana más que el promedio, o en las que todo el mundo gana lo mismo"
4.-Referencias
[1]- "Work Rules" by Laszlo Bock, april 2015
[2]- "The Best & the Rest: Revisiting the Norm of Normality of Individual Performance", Ernest O’Boyle Jr., Herman Aguinis, Publisher: Personnel Psychology, 2012, 65, 79-119


Muy triste, pero es la realidad. Bueno, Pareto es útil para empezar a separar el trigo de la paja.
ResponderEliminar